Optimization in deep learning

Part 1: The challenge

Optimization is a challenging problem in deep learning. Let’s suppose you have a large training data set, that is fairly representative of data you might see in the wild when running inference. That alone is no small feat¹. Now you need to choose a model architecture, train it, and hope it performs well on inference. Choosing a model architecture is itself a non-trivial endeavor, but let’s say you have a good candidate architecture. Maybe you choose an architecture that’s done well on similar models. Maybe you even have a good foundation model² that you’re fine-tuning. Training is fundamentally an optimization problem: find a set of model parameters that minimizes your training loss.

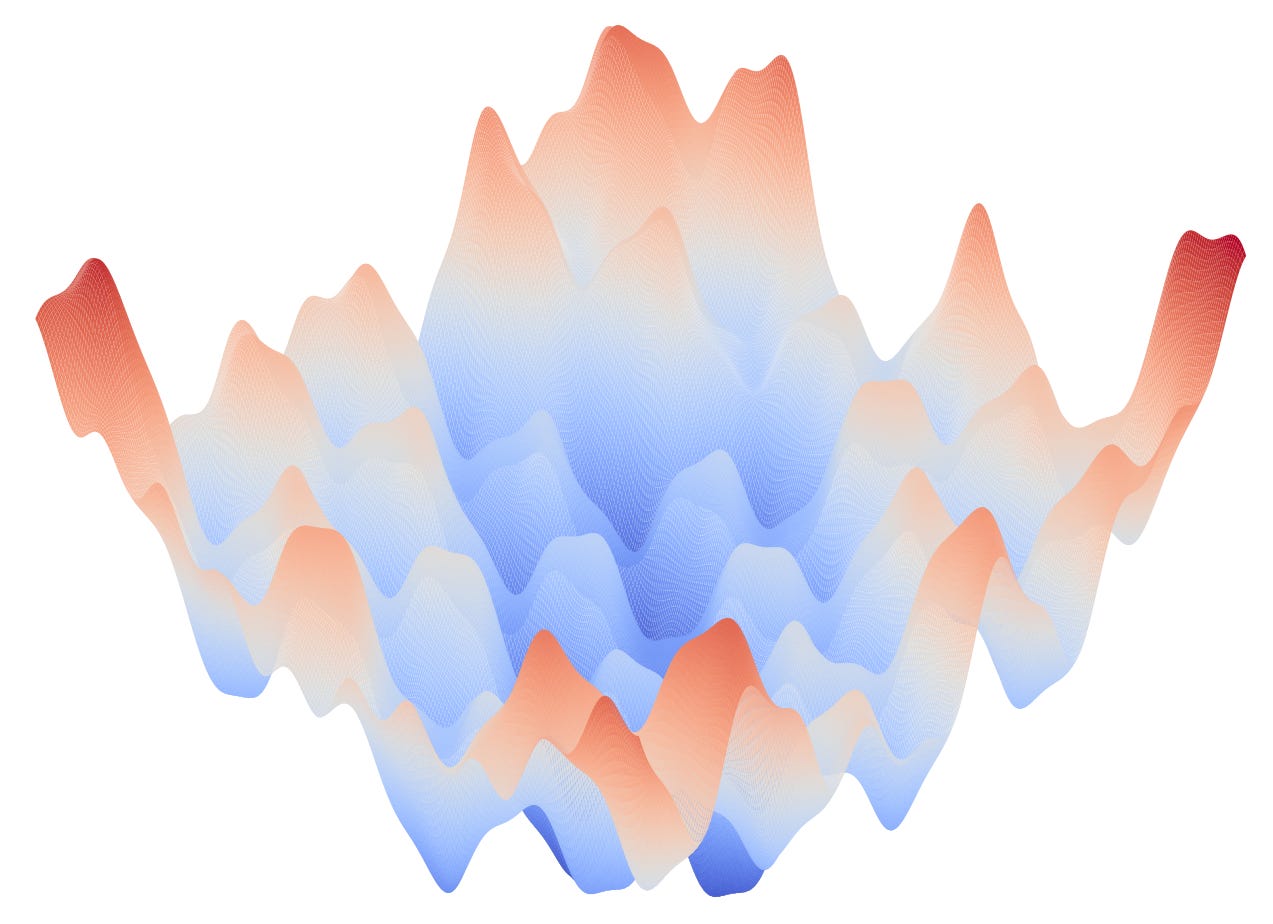
The primary goal of training to to pick the best parameters, with secondary goals to to find these parameters fast and with minimal resources. All three of these goals compete with one another. This is a hard problem. Ultimately, you’re using convex optimization techniques to solve a non-convex optimization problem. The loss surface you’re trying to find a minimum for might look kind of crazy; imagine something like this:

Note, this is just a fake objective function. Pavel, et al.³ created some visualizations of real objective functions in deep neural nets that make it clear this visualization isn’t particularly far off from objective functions you may encounter in the wild. Keep in mind though, that this objective function has only two variables. A neural net with millions, or even billions⁴, of parameters can have types of complexity that are impossible to really visualize like this.

Just looking at this, it’s clear that the risk of converging to a local minimum is quite real. Converging to a local minimum isn’t necessarily a huge problem in and of itself. If a local minimum is close to a global minimum for example, the cost of getting it wrong might not be that high on inference, assuming the training data is fairly representative of the test. That said, even “good” local minimum can slow down training, since techniques like mini-batch gradient descent⁵ are used in part to avoid getting stuck in local minimum. When the algorithm gets near a local minimum, it may hang out around there for a while before jumping out, since the gradient is flat their.

Saddle points are another problem. Like local minimum, they can slow down optimizers, due to their flat gradients. In the high-dimensional loss functions common in neural networks, saddle points are much more common than local minimum⁶.

Yet another problem is “sharp” minima. Informally, a sharp minimum is one where a small change in parameters yields a large change in the loss function near the minimum. More formally, a sharp minimum is one where ∇²f(x_min), the second-derivative matrix of the loss function at the minimum, has large positive eigenvalues⁷. Because of this sensitivity, and because training data will never perfectly represent inference data, sharp minima degrade generalization quality.

In the next few posts, I’m going to explore techniques that can be used to mitigate some of these issues. As you’ll see, much of the standard deep learning toolkit is really focused on this problem. I’ll look at the role of batch size in mini-batch gradient descent, advanced optimizer techniques, normalization techniques, and other optimization innovations.

1. Northcutt, Curtis G., Anish Athalye, and Jonas Mueller. "Pervasive Label Errors in Test Sets Destabilize Machine Learning Benchmarks." arXiv, 26 Mar. 2021, https://arxiv.org/abs/2103.14749.

2. Bommasani, Rishi, et al. "On the Opportunities and Risks of Foundation Models."arXiv, 16 Aug. 2021, https://arxiv.org/abs/2108.07258.

3. Izmailov, Pavel, et al. "Averaging Weights Leads to Wider Optima and Better Generalization." arXiv, 28 Dec. 2017, https://arxiv.org/abs/1712.09913.

4. Roser, Max, et al. "Exponential Growth of Parameters in Notable AI Systems." Our World in Data, https://ourworldindata.org/grapher/exponential-growth-of-parameters-in-notable-ai-systems. Accessed 30 May 2025.

5. Y. Lecun, L. Bottou, Y. Bengio and P. Haffner, "Gradient-based learning applied to document recognition," in Proceedings of the IEEE, vol. 86, no. 11, pp. 2278-2324, Nov. 1998, doi: 10.1109/5.726791.

6. Yann N. Dauphin, Razvan Pascanu, Caglar Gulcehre, Kyunghyun Cho, Surya Ganguli, and Yoshua Bengio. 2014. Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. In Proceedings of the 28th International Conference on Neural Information Processing Systems - Volume 2 (NIPS'14), Vol. 2. MIT Press, Cambridge, MA, USA, 2933–2941.

7. Keskar, Nitish Shirish, et al. "On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima." International Conference on Learning Representations (ICLR), 2017, https://arxiv.org/abs/1609.04836.